Description

在宽广的非洲荒漠中，生活着一群勤劳勇敢的羊驼家族。被族人恭称为“先知”的 Alpaca L. Sotomon 是这个家族的领袖，外人也称其为“所驼门王”。所驼门王毕生致力于维护家族的安定与和谐，他曾亲自率军粉碎河蟹帝国主义的野蛮侵略，为族人立下赫赫战功。所驼门王一生财宝无数，但因其生性节俭低调，他将财宝埋藏在自己设计的地下宫殿里，这也是今天 Henry Curtis 故事的起点。Henry 是一个爱财如命的贪婪家伙，而又非常聪明，他费尽心机谋划了这次盗窃行动，破解重重机关后来到这座地下宫殿前。

整座宫殿呈矩阵状，由 R×C 间矩形宫室组成，其中有 N 间宫室里埋藏着宝藏，称作藏宝宫室。宫殿里外、相邻宫室间都由坚硬的实体墙阻隔，由一间宫室到达另一间只能通过所驼门王独创的移动方式——传送门。所驼门王为这 N 间藏宝宫室每间都架设了一扇传送门，没有宝藏的宫室不设传送门，所有的宫室传送门分为三种:

  1. “横天门”：由该门可以传送到同行的任一宫室;

  2. “纵寰门”：由该门可以传送到同列的任一宫室;

  3. “自由门”：由该门可以传送到以该门所在宫室为中心周围8格中任一宫室(如果目标宫室存在的话)。

深谋远虑的 Henry 当然事先就搞到了所驼门王当年的宫殿招标册，书册上详细记录了每扇传送门所属宫室及类型。而且，虽然宫殿内外相隔，但他自行准备了一种便携式传送门，可将自己传送到殿内任意一间宫室开始寻宝，并在任意一间宫室结束后传送出宫。整座宫殿只许进出一次，且便携门无法进行宫室之间的传送。不过好在宫室内传送门的使用没有次数限制，每间宫室也可以多次出入。 现在 Henry 已经打开了便携门，即将选择一间宫室进入。为得到尽多宝藏， 他希望安排一条路线，使走过的不同藏宝宫室尽可能多。请你告诉 Henry 这条路 线最多行经不同藏宝宫室的数目。

Input

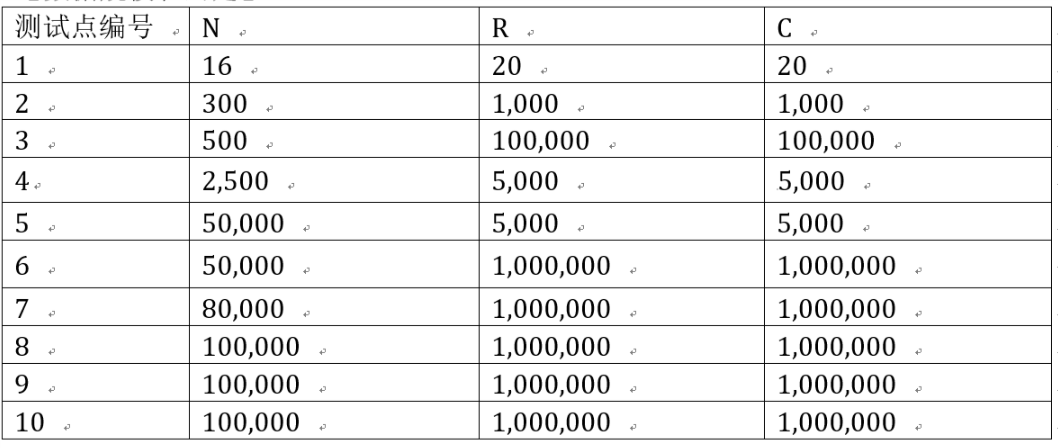
第一行给出三个正整数 N， R， C。 以下 N 行，每行给出一扇传送门的信息，包含三个正整数 xi， yi， Ti，表示该 传送门设在位于第 xi 行第 yi 列的藏宝宫室，类型为 Ti。Ti 是一个 1~3 间的整数， 1 表示可以传送到第 xi 行任意一列的“横天门”，2 表示可以传送到任意一行第 yi 列的“纵寰门”，3 表示可以传送到周围 8 格宫室的“自由门”。 保证
1≤xi≤R，1≤yi≤C，所有的传送门位置互不相同。

Output

只有一个正整数,表示你确定的路线所经过不同藏宝 宫室的最大数目。

Sample Input

1
2
3
4
5
6
7
8
9
10
11
10 7 7 
2 2 1 
2 4 2 
1 7 2 
2 7 3 
4 2 2 
4 4 1 
6 7 3 
7 7 1 
7 5 2 
5 2 1

Sample Output

1
9

Sample Input 图示：

列/行 1 2 3 4 5 6 7
1 2
2 1 2 3
3
4 2 1
5 1
6 3
7 2 1

Hint

Data Range

分析

这道题看似恐怖，实际上如果我们根据途中宝藏门的特点，将图建好之后，就是一道有向图的动态规划题，先说建好图后如何求出最大的藏宝路线

对于一张建好了的有向图 $G1$，首先求出这个图的强连通分量，那么 Henry 可以在这个强连通分量里面随意穿梭，但是只能得到强连通分量所包含的点的数量的宝藏，将强连通分量缩点，根据每一个强连通分点建新图 $G2$，此时 $G2$ 一定是一个有向无环的 DAG 图，那么我们只需要在这个 DAG 图上进行 DFS 来看，以每个点作为起点，能遍历到多少不同的点就可以了，注意这个图可能本身不连通，因此要主程序中枚举所有的强连通分点来 DFS，最后取最大值

那么接下来就是如何构建图 $G1​$ 了

根据题目的极限数据有 $100,000​$ 个点，如果每两个点之间都连一条边，那么边数最多将会达到$100,000\times (100,000-1)​$，毫无疑问会造成 MLE，这个时候我们发现：如果在一行上有多个横天门，那么只需要将其中的一个横天门与剩下的点连边，然后将剩下的横天门与这个横天门连边，就能保证一行上的所有横天门都能到达这一行上的所有点，纵寰门同理

那么极限情况下（全部是横天门，或者纵寰门），除去自由门，只需要记录 $N\times 2$ 条边就完事儿了，最后的自由门没有优化技巧，只能按照八个方向依次加边，因此边集数组的大小是：$8\times N$，$N$ 表示点数极限

在建图 $G1​$ 的时候，按照上述思路，需要记录各点的坐标（x，y），记录各行上的点，各列上的点（用 Vector 实现），记录各个点的一维编号（为自由门加边做准备），只需要取各行各列的第一个横天门（或者纵寰门）来加边，其他门加到它们上面去即可

各个点的一维编号是用 x 坐标乘上 maxrow 加上 y 坐标来表示，这种方法在用回溯解决数独问题的时候也用过（题目链接：P1194 【训练题】数独）

Codes

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
#pragma GCC optimize(3)
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <cstdio>
#include <map>
#define maxn 100001
#define maxr 1000001
using namespace std;
typedef long long ll;
struct node{
	int to,nxt;
}g[maxn*8],g2[maxn*8]; int tot,tot2;
int head[maxn],head2[maxn];
int n,R,C,T[maxn],posx[maxn],posy[maxn];
int low[maxn],dfn[maxn],dt;
int cp[maxn],cpt[maxn]; stack<int> stk;
int f[maxn]; // dp array 
bool ins[maxn];
vector<int> rs[maxr],cs[maxr];
map<ll,int> M;
int offsetX[]={-1,1,0,0,-1,1,-1,1};
int offsetY[]={0,0,-1,1,-1,1,1,-1};
ll convert(int x,int y){
	return (ll)x*maxr+y;
}
inline void Einsert(int x,int y){
	if(x==y) return;
	g[++tot].nxt=head[x];
	g[tot].to=y; head[x]=tot;
}
inline void Einsert2(int x,int y){
	if(x==y) return;
	g2[++tot2].nxt=head2[x];
	g2[tot2].to=y; head2[x]=tot2;
}
inline void _firstbuild(){
	int sig=0,vlen;
	// for rows 
	for(int i=1;i<=R;i++){
		sig=0; vlen=rs[i].size();
		for(int j=0;j<vlen;j++)
			if(T[rs[i][j]]==1){sig=rs[i][j];break;}
		if(sig){
			for(int j=0;j<vlen;j++){
				Einsert(sig,rs[i][j]);
				if(T[rs[i][j]]==1)Einsert(rs[i][j],sig);
			}
		}
	}
	// for cols 
	for(int i=1;i<=C;i++){
		sig=0; vlen=cs[i].size();
		for(int j=0;j<vlen;j++)
			if(T[cs[i][j]]==2){sig=cs[i][j];break;}
		if(sig){
			for(int j=0;j<vlen;j++){
				Einsert(sig,cs[i][j]);
				if(T[cs[i][j]]==2)Einsert(cs[i][j],sig);
			}
		}
	}
	// for 9ggs 
	int newx,newy;
	for(int i=1;i<=n;i++)
		if(T[i]==3){
			for(int j=0;j<8;j++){
				newx=posx[i]+offsetX[j]; 
				newy=posy[i]+offsetY[j];
				if(M[convert(newx,newy)]){
					Einsert(M[convert(posx[i],posy[i])],M[convert(newx,newy)]);
				}
			}
		}
}
inline void _secondbuild(){
	int k;
	for(int i=1;i<=n;i++)
		for(int j=head[i];j;j=g[j].nxt){
			k=g[j].to;
			if(cp[i]!=cp[k])
				Einsert2(cp[i],cp[k]);	
		}
} 
void tarjan(int u){
	low[u]=dfn[u]=++dt; stk.push(u);
	int v; ins[u]=true;
	for(int i=head[u];i;i=g[i].nxt){
		v=g[i].to;
		if(!dfn[v]){
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else{
			if(ins[v]) low[u]=min(low[u],dfn[v]);
		}
	}
	if(dfn[u]==low[u]){
		int shead; cp[0]++;
		do{
			shead=stk.top(); stk.pop();
			cp[shead]=cp[0];
			cpt[cp[0]]++; ins[shead]=false;
		}while(shead!=u);
	}
}
int dfs(int u){
	if(f[u]) return f[u]; int v;
	for(int i=head2[u];i;i=g2[i].nxt){
		v=g2[i].to;
		f[u]=max(f[u],dfs(v));
	}
	return f[u]=f[u]+cpt[u];
}
int main(){
	#ifndef ONLINE_JUDGE
	freopen("soto.in","r",stdin);
	freopen("soto.out","w",stdout);
	#endif
	cin>>n>>R>>C;
	for(int i=1;i<=n;i++){
		cin>>posx[i]>>posy[i]>>T[i];
		rs[posx[i]].push_back(i);
		cs[posy[i]].push_back(i);
		M[convert(posx[i],posy[i])]=i;
	}
	_firstbuild();
	for(int i=1;i<=n;i++)
		if(!dfn[i]) tarjan(i);
	_secondbuild();
	int ans=0;
	for(int i=1;i<=cp[0];i++)
		if(!f[i]) ans=max(ans,dfs(i));
	cout<<ans;
	return 0;
}